Basics - “Finding the Pose” of a Photo
It is possible to place a photo in a 3D model in such a way that it appears seamlessly aligned with the model, and the best way to illustrate this is by a real-world example. Suppose, on a sunny summer day, you take a photo using a tripod in a park. Let’s say the tripod remains in the same spot while you run off to get your photograph made into a transparency. On your return, you take a transparency viewer that allows you to view the transparency overlaid on whatever is behind it in the background and place it on the tripod. You aim it in the same direction (and assume that the lens of the viewer matches the lens properties on the original camera), insert your transparency, and – voila! – everything in your photo is perfectly aligned with the actual background of the park.
It is important to note that if the tripod had been moved between the act of taking the photo and viewing it, everything might not line up. Strictly speaking, there is only one spot and one camera direction where everything is aligned. In computer vision, this alignment of camera and image is known as the “pose” of the photo. Knowing the pose of a photo is essential if it is to be correctly positioned in any 3D world, whether real or virtual.
It is also important to note that not everything in any photo may actually be aligned. People move, the shifting position of the sun alters lighting conditions and shadows, and seasons change. Over deep time, buildings and cityscapes also change, as do terrain and landscape. Practitioners of “Rephotography,” the act of re-aligning cameras to take duplicate images in new conditions, are interested in viewing the differences wrought by time or conditions. They align their cameras with those of earlier photographers and, using the same position and camera lens, take a new picture, matching an earlier image. Toggling back and forth between the two images allows viewers to witness the changes between the original and the new, an experience that can be magical [1]. An equally magical effect happens with aligned projection on physical scenes, as has been exhibited in an art installation involving a projected living room painted white [2].
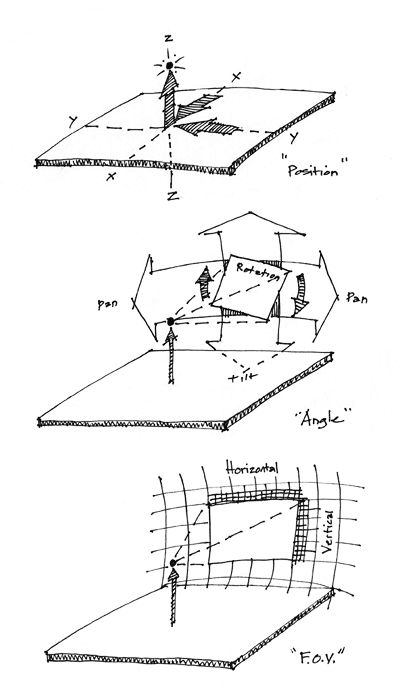
Figure 1. Three sets of parameters needed to pose a photo in 3D.
Technically, finding the pose of a photo requires knowing three sets of principal parameters. The first set is the camera’s position in space, generally referred to as x, y, and z or latitude, longitude, and altitude. The next set is the angular direction (or orientation) of the camera, usually called pan, tilt, and rotation (also known as yaw, pitch, and roll; also, pan and tilt correspond to azimuth and elevation). Finally, there is the field of view (FOV) of the camera, sometimes called scale, zoom, or focal length; this can be expressed either as horizontal and vertical FOV, or as a single FOV along with the aspect ratio of the frame. The total number of parameters needed to pose a photo, then, is eight: three for position, three for angle, and two for FOV. If the aspect ratio is known and constant (such as 3:2 for digital still cameras or 16:9 for HDTV), then the FOV can be expressed as a single parameter; as a result, a total of seven parameters is needed to pose a photo.
Other secondary parameters exist as well, including the rectilinearity of the optics, the “center of projection” in the image, and the degree of focus and resolution of the photo. For most cameras, however, with center-mounted aspheric lenses (in which straight lines in the world appear straight in the resulting image) and adequate resolution and depth of field, the seven principal parameters are generally enough.
What degree of accuracy do we need in order to pose a photo in a 3D model so that it acquires the same magic as rephotography? This remains an open question and is certainly partially subjective, but we propose a maximum error of one meter for position and one degree for orientation. Cameras are now available with built-in GPS (which provides position), and some digital cameras already include tilt sensors, used to distinguish between horizontal and vertical photos. Further, cheap angular sensors are common in a variety of consumer applications that will eventually migrate into cameras. Finally, the EXIF (Exchangeable Image File Format) specifications allow a camera to store in the JPEG picture file information such as date and time, description, camera settings, and even geolocation data in a pseudo-standard way.
Most consumer-level GPS devices are accurate to three or four meters, and cheap angular sensors cannot resolve beyond several degrees at best; thus, neither are currently accurate enough to effectively pose photographs. At the other extreme are expensive, specialized motion control cameras and match moving software for the Hollywood special effects industry, where accuracy must be within a few millimeters and within a fraction of a degree (and where many of the secondary parameters also need to be taken into account). Thus, our needs lie somewhere between current consumer technologies and specialized, expensive professional gear.


